F2BLib — Function to Bytecode Library
TL;TR
Parse mathematical function expressions, convert them to Java bytecode, and evaluate them very quickly.
Introduction
F2BLib – Function to Bytecode Library – defines a Grammar for real-valued mathematical function expressions. It parses an input source using Antlr4 and converts the resulting abstract syntax tree (AST) to Java bytecode using ASM. The functions can then be evaluated very fast.
Example of an abstract syntax tree:
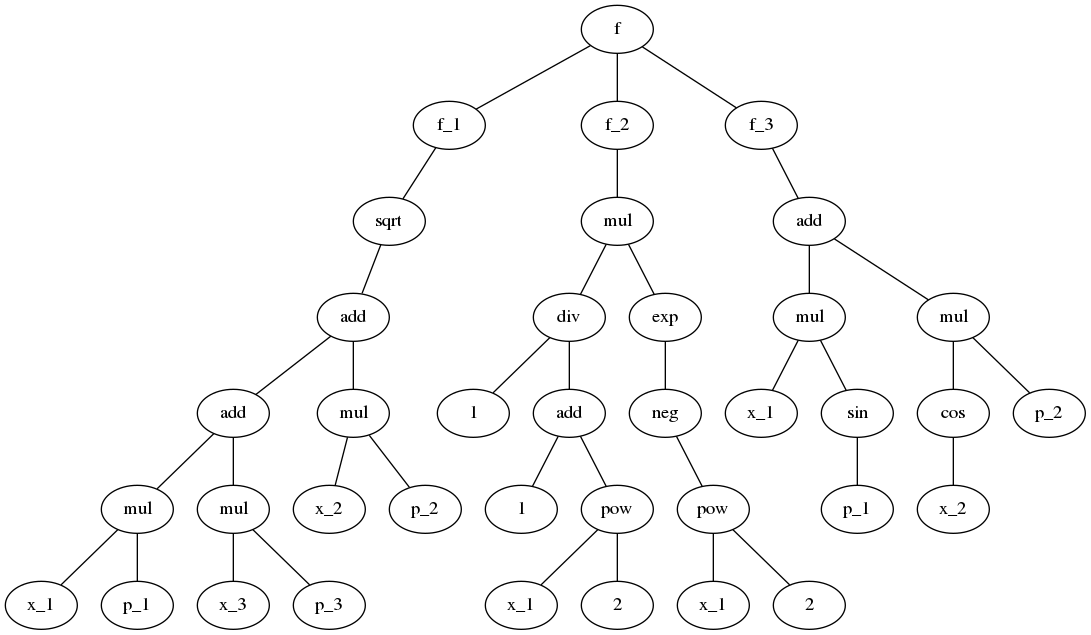
By real-valued mathematical functions we mean mappings of the form

Getting Started
Suppose you want to evaluate a real-valued function with two variables and two parameters:

Introduce the dependency
com.github.drstefanfriedrich.f2blib:f2blib:${f2blibVersion}
with the correct version of F2BLib you want to use into your Gradle build.gradle.
Then define a function like in
private static final String FUNCTION = "function some.packagename.SomeClassName;" +
"begin" +
" f_1 := p_1 * sin(x_1) + x_2;" +
" f_2 := ln(p_2) + exp(x_2);" +
"end";
and obtain a reference to the Function Evaluation Kernel and load the function into the kernel:
FunctionEvaluationKernel kernel = new FunctionEvaluationFactory().get().create();
kernel.load(FUNCTION);
Now you can start evaluating the function:
double[] x = new double[]{ 2.51, 1.28 };
double[] p = new double[]{ -1.45, 8.27 };
double[] y = new double[2];
kernel.eval("some.packagename.SomeClassName", p, x, y);
We refer to IntegrationTest.java.
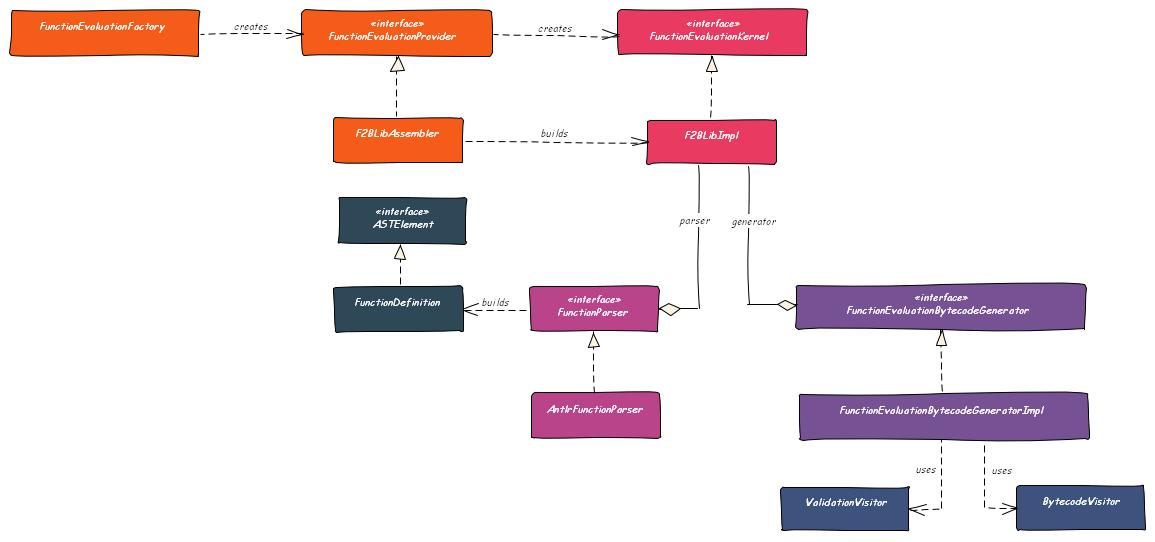
Architecture
The main components of the system interact as follows:
Build
To build the project and start developing, do
$ git clone git@github.com/DrStefanFriedrich/f2blib
$ cd f2blib
$ ./gradlew
To run the performance tests, do
$ ./gradlew -Dcom.github.drstefanfriedrich.f2blib.performancetest.enabled=true
Limitations
- Right now variables must be named x_i, where i is an integer and parameters must be named p_j, where j is an integer.
Finance Mathematics/Life Insurances
Lets consider a life insurance contract with the following conditions:
- At the beginning of the contract the policy holder is x years old
- The life insurance contract runs n years
- Every year the policy holder pays a specified fee denoted by F at the beginning of the year
- The fee F is a gross value. The net value will be calculated by reducing the value by an expense factor e.
- If the policy holder dies before the end of the contract, a death premium D will be paid to the bereaved at the end of the year the policy holder died
- If the policy holder reaches the end of the contract, an annuity A that is to be calculated, will be paid to the policy holder every year at the end of the year until its death
- The calculations will be done using a specified interest rate i, which is fixed
Let K be the rounded down number of years when the policy holder dies. Then K is a probability variable. If we denote by v = 1/(1+i) the discounting factor, we get for the benefit B discounted to the beginning of the contract (+ means money will be paid into the insurance, - means you get money out from the insurance):

By using a well known formula for the geometric series, we get

Crucial in life insurances are mortality tables.

denotes the probability that an x year old dies within one year. The expression 101 - x in the formula above results from the fact that typical mortality tables will be cut off at the age of 101. Then

is the probability that an x year old lives exactly for another k years and then dies within one year.
A life insurance is considered to be fair, if and only if the expected value is zero, which leads to

From the above formula an expression for the annuity A can easily be deduced, which is left to the reader as an exercise. For the impatient, we refer to the package
com.github.drstefanfriedrich.f2blib.lifeinsurance
under src/test/java.
Performance Tests
We carried out a few performance tests to demonstrate the capabilities of F2BLib.
The hardware used to perform the test was an ASUS notebook running Fedora 23 Linux
with a 2.4 series kernel. The CPU of the notebook is a Intel Core i7-6700HQ with 2.6
GHz. We used JDK 11.0.4. The test setup was as follows: we executed the script
performance-test.sh, analyzed the log file performance-test.log and calculated
the Mean and Standard Deviation from here.
We performed the following test cases:
Test Case 1: BytecodeVisitorImplTest
On one thread a lot of ‘nonsense’ functions will be evaluated. This test case uses the bytecode visitor.
Test Case 2: EvalVisitorImplTest
Same as Test Case 1, but this time using the EvalVisitor.
Test Case 3: BytecodePerformanceTest
This test case uses two queues. One request queue and one response queue. One worker thread fills the request queue and a specified number of worker threads listen on the request queue, dequeue elements, process them, and write the result to the response queue. This test case uses the bytecode visitor.
Test Case 4: EvalPerformanceTest
Same as Test Case 3, but this time using the EvalVisitor.
Test Case 5: BytecodeLifeInsuranceVariantsTest
This test case starts a specified number of worker threads and executes on each thread a lot of different life insurances calculations. The bytecode visitor is used.
Test Case 6: EvalLifeInsuranceVariantsTest
Same as Test Case 5, but this time using the EvalVisitor.
Test Case 7: JavaLifeInsuranceVariantsTest
Same as Test Case 5, but this time using a plain Java implementation of the life insurance formula.
The result was as follows:
| Test Case | Duration (secs) | Standard Deviation |
|---|---|---|
| BytecodeVisitorImplTest | 2.095 | 0.02465 |
| EvalVisitorImplTest | 16.455 | 0.5356 |
| BytecodePerformanceTest | 1.852 | 0.05596 |
| EvalPerformanceTest | 32.948 | 1.904 |
| BytecodeLifeInsuranceVariantsTest | 0.3727 | 0.01523 |
| EvalLifeInsuranceVariantsTest | 58.300 | 2.682 |
| JavaLifeInsuranceVariantsTest | 0.3637 | 0.03246 |
References
Parser Generators
Here is a list of parser generators. We used the list during evaluation of the different frameworks.
We decided to use Antlr, because it is very well known and popular. In contrast, Xtext is much more powerful and has a lot of features we don’t need.
Bytecode Generation
Here is a list of Java bytecode generation frameworks. We used the list during evaluation of the different frameworks.
ByteBuddy as well as cglib extend ASM. ByteBuddy is optimized for runtime speed. ASM is very small, very fast, has no dependencies to other libraries, and is a low-level bytecode generation system. It also has a class called ASMifier which can transform arbitrary .class files to .java files containing all the ASM statements needed to reproduce the class. For the last reason we chose ASM.
Arithmetic Expression Evaluation
Here is a list of mathematical expression evaluation frameworks similar to this one:
Finance Mathematics
- Volkert Paulsen: Versicherungsmathematik (only available in German)
- Michael Koller: Lebensversicherungsmathematik (only available in German)
- Michael Koller: Stochastische Modelle in der Lebensversicherung, Springer, ISBN 978-3-642-11252-2
- Hartmut Milbrodt, Manfred Helbig: Mathematische Methoden der Personenversicherung, de Gruyter, 1999.
- Hansjörg Albrecher: Finanz- und Versicherungsmathematik 1
- Actuarial Notation
- Actuarial Present Value
- Lebensversicherungsmathematik
License
The project is published under the Eclipse Public License v2.0, which is online available at this URL.




